answer : False
The measure of a tangent-tangent angle is one - half the difference of the measures of the intercepted arcs.
The diagram is attached below
AB and BC are the two tangents
By exterior angle theorem
∠3 = ∠2 + ∠4
So ∠2 = ∠3 - ∠4
Now we find angle 3 and 4, we know when a chord and tangent intersect at a point then the measure of angle is one half of measure of intercepted arc
∠3 =
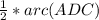
∠4 =

∠2 = ∠3 - ∠4
∠2 =
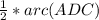 -
-

∠2 =
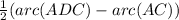
The measure of a tangent-tangent angle is one half the difference of the measures of the intercepted arcs.