Question

For what values of a and m does f(x) have a horizontal asymptote at y = 2 and a vertical asymptote at x = 1?

f(x)=2x^m/x+a

which is the answer

a = –1, m = 0
a = 1, m = 0
a = –1, m = 1
a = 1, m = 1

Answer 1

C

Explanation:

a= -1, m=1

Answer 2

`f(x)` will have a horizontal asymptote of
`y=2` if


`\displaystyle\lim_(x\to\pm\infty)(f(x)-2)=0`

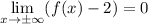
where at least one of these limits needs to be satisfied. Since we would like



`(2x^m)/(x+a)-2=(2x^m-2(x+a))/(x+a)`

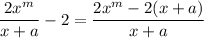
to converge to 0, we need the
`x^m` term to disappear in the numerator. The only way for that to happen is if
`m=1`. Then


`(2x-2(x+a))/(x+a)=-(2a)/(x+a)`

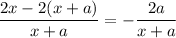
and this does indeed approach 0 as
`x` gets arbitrarily large.

Now, in order to have a vertical asymptote at
`x=1`, all we need to do is set
`a=-1`. Then


`\displaystyle\lim_(x\to-1)(2x)/(x+1)`

does not exist, as required.