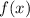
will have a horizontal asymptote of
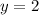
if
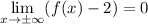
where at least one of these limits needs to be satisfied. Since we would like
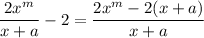
to converge to 0, we need the
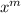
term to disappear in the numerator. The only way for that to happen is if
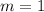
. Then
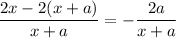
and this does indeed approach 0 as

gets arbitrarily large.
Now, in order to have a vertical asymptote at
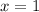
, all we need to do is set

. Then
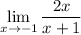
does not exist, as required.