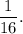Answer: The required correct value is
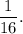
Step-by-step explanation: We are given to find the correct value so that the following expression is a perfect square trinomial :

Let the required number be represented by p.
Then, we have

So, to make the given expression a perfect square trinomial, we must have
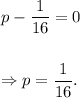
Thus, the required correct value is