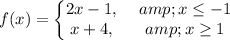Question

Select the correct answer from each drop-down menu.

~look at picture~

The graph represents the piecewise function

Answer 1

`f(x)=\left\{\begin{matrix}2x-1,\ & x\leq -1\\ x+4,\ & x\geq 1\end{matrix}\right.`

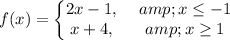
Explanation:

From the graph, we see that,

The function is divided with domain being
`x\leq -1` and
`x\geq 1`.

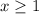The general form of a straight line is
`y=mx+b`, where m= slope and b= y-intercept.

So, we have,

1. In the region when
`x\leq -1`, the function passes through the points (-1,-3) and (-2,-5).

The slope is given by
`m=(-5+3)/(-2+1)=(-2)/(-1)=2`

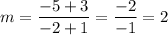
Substituting m= 2 and point (-1,-3) in the general form gives us,

`-3=2* -1+b\\\\-3+2=b\\\\b=-1`

Thus, the equation of the line is
`y=2x-1`.

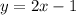2. In the region when
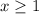`x\geq 1`, the function passes through the points (1,5) and (2,6).

The slope is given by
`m=(6-5)/(2-1)=1`

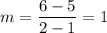
Substituting m= 1 and point (1,5) in the general form gives us,

`5=1* 1+b\\\\5-1=b\\\\b=4`

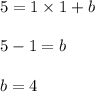
Thus, the equation of the line is
`y=x+4`.

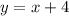Hence, the piece wise function is given by
`f(x)=\left\{\begin{matrix}2x-1,\ & x\leq -1\\ x+4,\ & x\geq 1\end{matrix}\right.`

Answer 2

The left line segment has slope 2 and includes the point (-1, -3). The right line segment has slope 1 and includes the point (1, 5). The function can be written as ...


`f(x)=\left\{\begin{array}{rcl}2x-1&\mbox{if}&x\le-1\\x+4&\mbox{if}&x\ge1\end{array}\right\,`