Answer:
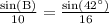
Explanation:
Please find the attachment.
We have been given that in triangle ABC, side
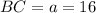 , side
, side
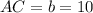 and measure of angle A is 42 degrees. We are asked to find an equation that can be used to find the measure of angle B.
and measure of angle A is 42 degrees. We are asked to find an equation that can be used to find the measure of angle B.
We will use law of sines to solve our given problem.
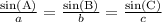
Upon substituting our given values, we will get:
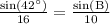
Switch sides:
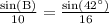
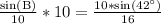
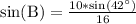
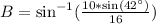
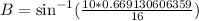
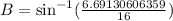
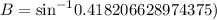
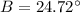
Therefore, the equation
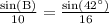 can be used to find m angle B.
can be used to find m angle B.