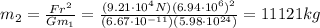The gravitational force between two objects is given by:
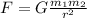
where
G is the gravitational constant
m1 and m2 are the masses of the two objects
r is the separation between the two objects
The distance of the telescope from the Earth's center is
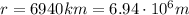
, the gravitational force is
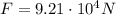
and the mass of the Earth is
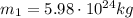
, therefore we can rearrange the previous equation to find m2, the mass of the telescope: