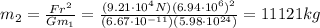Question

The center of the Hubble space telescope is 6940 km from Earth’s center. If the gravitational force between Earth and the telescope is 9.21 × 104 N, and the mass of Earth is 5.98 × 1024 kg, what is the mass of the telescope? Round the answer to the nearest whole number.

Answer 1

11121 kg is the answer

Answer 2

The gravitational force between two objects is given by:

`F=G (m_1 m_2)/(r^2)`
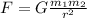
where
G is the gravitational constant
m1 and m2 are the masses of the two objects
r is the separation between the two objects

The distance of the telescope from the Earth's center is
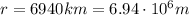
`r=6940 km=6.94 \cdot 10^6 m`, the gravitational force is
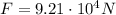
`F=9.21 \cdot 10^4 N` and the mass of the Earth is
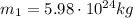
`m_1=5.98 \cdot 10^(24) kg`, therefore we can rearrange the previous equation to find m2, the mass of the telescope:

`m_2 = (Fr^2)/(Gm_1)= ((9.21 \cdot 10^4 N)(6.94\cdot 10^6)^2)/((6.67\cdot 10^(-11))(5.98\cdot 10^(24))) =11121 kg`