Question

Define the type of sequence below. 7, 14, 28, 56, 122, ...

Answer 1

the sequence is a geometric sequence

Answer 2

Answer: The given sequence is a GEOMETRIC sequence with first term 7 and common ratio 2.

Step-by-step explanation: We are given to define the type of the following sequence :

7, 14, 28, 56, 122, . . .

Let us denote the n-th ter of the given sequence by
`a_n.`

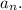
Then, we see the following relation between the consecutive terms of the given sequence :

`(a_2)/(a_1)=(14)/(7)=2,\\\\\\(a_3)/(a_2)=(28)/(14)=2,\\\\\\(a_4)/(a_3)=(56)/(28)=2,\\\\\\(a_5)/(a_4)=(122)/(56)=2,\\\\\\\vdots~~~~~~\vdots`

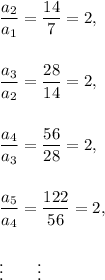
Therefore, we get

`(a_2)/(a_1)=(a_3)/(a_2)=(a_4)/(a_3)=(a_5)/(a_4)=~~.~~.~~.~~=2.`

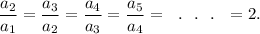
That is, there is a common ratio of 2 between any two consecutive terms of the sequence.

Thus, the given sequence is a GEOMETRIC sequence with first term 7 and common ratio 2.