Question

Find the x-intercept of the parabola with vertex (-3,-14) and y-intercept (0,13)

Answer 1

Did u end up finding the answer. I'm working on the same one RN

Answer 2

If there is one x-intercept, then there is 2. First we have to use the information given to write the equation for the parabola. Then we can factor it, because factoring is what finds the zeros (aka x-intercepts, roots, and solutions) of the function. We know from the fact that the y-intercept is above the vertex that this is an upwards-opening parabola. The standard form of a parabola of this nature is
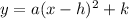
`y=a(x-h) ^(2)+k`. We have the h and k from the given vertex, and we have the x and y from the y-intercept. We will use all that to solve for a.
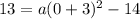
`13=a(0+3) ^(2) -14`. When we simplify that down we get 13 = 9a - 14 and 9a = 27. Therefore, a = 3. Now we can write the equation for the parabola.
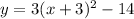
`y=3(x+3) ^(2)-14`. But we can't solve for x the way it is without simplifying that completely. We need to expand that binomial, and when we do that we have
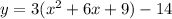
`y=3( x^(2) +6x+9)-14`. Then we have to distribute in the 3 and then subtract 14 at the end. That will give us, finally,
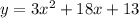
`y=3 x^(2) +18x+13`. Now we can set that equal to 0 and factor it. The x-intercepts exist when y = 0; when y = 0, we have x-values only, which are the places where the graph goes through the x-axis. Putting those values into the quadratic formula, we find the 2 zeros of the function are x = -.839 and -5.16