Question

Find the perimeter of triangle ABC.

9 sqrt 84
9 sqrt 2-sqrt 82
18+sqrt 82
none of the above.
the coordinates of the triangle are (2,2) (6,6) (7,-3)

Answer 1

the correct answer is the second (b) choice

9rad2 + rad82

i just took the test and got it right

Answer 2

By definition, the perimeter of the triangle is the sum of its sides.
We must then use the formula of distance between points:

`d = √((x2-x1) ^ 2 + (y2-y1) ^ 2)`
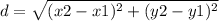
We now look for the longitus for each of the sides:

For L1:

`L1 = √((6-2)^2 + (6-2)^2)`

`L1 = √(32)`

`L1 = 4√(2)`

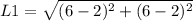
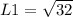
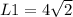
For L2:

`L2 = √((7-2)^2 + (-3-2)^2)`

`L2 = √(50)`

`L2 = 5√(2)`

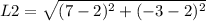
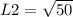
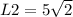
For L3:

`L3 = √((7-6)^2 + (-3-6)^2)`

`L3 = √(82)`

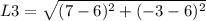
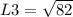
Then, the perimeter is given by:
P = L1 + L2 + L3
Substituting values we have:

`P = 4√(2) + 5√(2) + √(82) P = 9√(2) + √(82)`

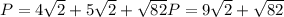Answer:
the perimeter of triangle ABC is:
none of the above.