Answer:
![2\sqrt[3]{3}-\sqrt[3]{18}](https://img.qammunity.org/2019/formulas/mathematics/high-school/7j12d57isixx7dnw3mgm7za9d8budmes6f.png)
Step-by-step explanation:
We first rationalize the denominator. This means we multiply the numerator and denominator by a factor that will make the denominator a whole number.
Our denominator is
![\sqrt[3]{9}](https://img.qammunity.org/2019/formulas/mathematics/high-school/jrfdok4h3dlybf5es3f9m8us6qz53hg8hr.png) ; this can also be written as
; this can also be written as
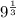 .
.
For 9 to be a whole number, its exponent must be a whole number. We want to add 2/3 to the exponent of 9 on the bottom; this means we multiply by
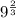 :
:
On the numerator, this gives us:
6(9^(2/3))-3(6^(1/3))(9^(2/3))
=
![6\sqrt[3]{9(9)} -3\sqrt[3]{2(3)}(\sqrt[3]{9(9)}) \\\\=6\sqrt[3]{3(3)(3)(3)}-3\sqrt[3]{2(3)(3)(3)(3)(3)}\\\\=6(3)\sqrt[3]{3}-3(3)\sqrt[3]{2(3)(3)}\\\\=18\sqrt[3]{3}-9\sqrt[3]{18}](https://img.qammunity.org/2019/formulas/mathematics/high-school/rqxiqw7pbv02tcqpzhbrwrgjdcajeyf6po.png)
On the denominator, we will have:
(9^(1/3))(9^(2/3)) = 9^(3/3) = 9^1 = 9
This gives us:
![\frac{18\sqrt[3]{3}-9\sqrt[3]{18}}{9}\\\\=2\sqrt[3]{3}-\sqrt[3]{18}](https://img.qammunity.org/2019/formulas/mathematics/high-school/xr85ff3sspnkj0izlucbdharmnbemg0hhm.png)