Question

What is the following quotient 6-3(^3√6)/^3√9

Answer 1

Quotient given:


`\frac{6-3 \sqrt[3]{6} }{ \sqrt[3]{9} }`

Answer:


`2 \sqrt[3]{3} - \sqrt[3]{18}`

Step-by-step explanation:

1) Rationalize by multiplying numerator and denominator by
`\sqrt[3]{9}`

2)

`\frac{6-3 \sqrt[3]{6} }{ \sqrt[3]{9} } \frac{\sqrt[3]{9}}{\sqrt[3]{9}}`

3) Due the operations


`\frac{6 \sqrt[3]{3}-3 \sqrt[3]{6.3}}{ \sqrt[3]{27} }`


`\frac{6 \sqrt[3]{3}-3 \sqrt[3]{6.3}}{ 3 }=2 \sqrt[3]{3} - \sqrt[3]{18}`

Answer 2

`2\sqrt[3]{3}-\sqrt[3]{18}`

Step-by-step explanation:

We first rationalize the denominator. This means we multiply the numerator and denominator by a factor that will make the denominator a whole number.

Our denominator is
`\sqrt[3]{9}`; this can also be written as
`9^{(1)/(3)}`.

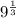For 9 to be a whole number, its exponent must be a whole number. We want to add 2/3 to the exponent of 9 on the bottom; this means we multiply by
`9^{(2)/(3)}`:

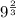On the numerator, this gives us:

6(9^(2/3))-3(6^(1/3))(9^(2/3))

=
`6\sqrt[3]{9(9)} -3\sqrt[3]{2(3)}(\sqrt[3]{9(9)})  \\\\=6\sqrt[3]{3(3)(3)(3)}-3\sqrt[3]{2(3)(3)(3)(3)(3)}\\\\=6(3)\sqrt[3]{3}-3(3)\sqrt[3]{2(3)(3)}\\\\=18\sqrt[3]{3}-9\sqrt[3]{18}`

On the denominator, we will have:

(9^(1/3))(9^(2/3)) = 9^(3/3) = 9^1 = 9

This gives us:

`\frac{18\sqrt[3]{3}-9\sqrt[3]{18}}{9}\\\\=2\sqrt[3]{3}-\sqrt[3]{18}`