Question

Find the exact area of the region bounded by two concentric circles with radii 10 inches and 6 inches.

Answer 1

Area of circle
A = pi r^2
A = pi(10^2 - 6^2)
bounded by both is 36 pi
bounded by anyone is 100 pi
bounded by one only is 64 pi

Answer is: 64 PI






Hope that helps!!!

Answer 2

Answer: The area of the region bonded by two concentric circles with radii 10 inches and 6 inches is
`64\pi` in²

Explanation:

Here, two circles having radius 10 inches and 6 inches are concentric,

Also, the area of the region bounded by these circles = Area of large circle - Area of small circle. ( Circle having greater radius is called large circle while having smaller area is called small circle )

=
`\pi (10)^2 - \pi(6)^2`

=
`\pi( 10^2 - 6^2)`

=
`\pi ( 100 - 36 )`

=
`64\pi\text{ square inches }`

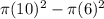
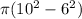
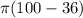
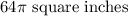
Hence, The area of the region bonded by two concentric circles with radii 10 inches and 6 inches is
`64\pi` in²