Question

Which value of b will cause the quadratic equation x^2+bx+5=0 to have two real number solution

Answer 1

To have 2 real number solutions the discriminant b^2 - 4ac must be greater than zero.

so the condition for 2 real roots in this equation is:-

b^2 - 4*1*5 > 0
b^2 > 20

b > sqrt 20 ( positive root) Answer

Answer 2

Every value of b>4.47 and b<-4.47 will cause the quadratic equation
`x^2+bx+5=0` to have two real number solution.

Explanation:

We have the quadratic function
`x^2+bx+5=0`, and we have to find the value of b.

A quadratic function is
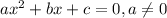`ax^2+bx+c=0, a\\eq 0`, a quadratic function usually has two real solutions. You can find that solutions using Bhaskara's Formula:

`x_1=(-b+√(b^2-4.a.c) )/(2.a)`

`x_2=(-b-√(b^2-4.a.c) )/(2.a)`

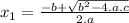
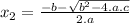
`x_1` and
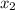`x_2` are real solutions of the quadratic equation if and only if:

`b^2-4.a.c >0`

If
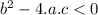`b^2-4.a.c <0` the quadratic equation doesn't have real solutions.

If
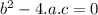`b^2-4.a.c =0` the quadratic equation has only one solution.

Then in this case to have two real number solutions:
`b^2-4.a.c >0`

We have
`x^2+bx+5=0`, where a=1, b, c=5

Then,

`b^2-4.a.c >0\\b^2-4.1.5>0\\b^2-20>0`

Adding 20 in both sides of the equation:

`b^2-20>0\\b^2-20+20>20\\b^2>20\\b>√(20)`

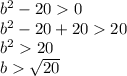
Which is the same as:
`b<-√(20)`

Then,
`b>√(20)\\b>4.47\\b<-√(20)\\b<-4.47`

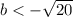
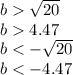
Then every value of b>4.47 and b<-4.47 will cause the quadratic equation
`x^2+bx+5=0` to have two real number solution.

For example b=-5 or b=5.

If you replace with b=-5 in
`b^2-4.a.c >0`

`b^2-4.a.c >0\\(-5)^2-4.1.5>0\\25-20>0\\5>0`

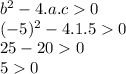
Then the quadratic function has two real number solutions.