Answer:
Axis of symmetry is x = -4.
Explanation:
The given equation is
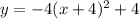
It represents a downward parabola because a = -4 <0
The vertex form of a parabola is
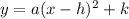
Where (h,k) is the vertex and x = h is the axis of symmetry.
Thus, the vertex of the given parabola is (-4,4) and the axis of symmetry is x = -4.
The vertex will be at (-4,4) and is the lowest point of the graph of the parabola.
The x-intercept are
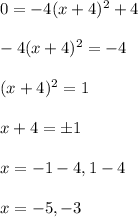
And the y-intercepts is
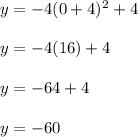
Thus, using these facts we can draw the graph which is shown below.
Axis of symmetry is x = -4.
D is the correct option.