Answer:
Option A is correct
Explanation:
Given that Peter placed a survey on his blog asking whether users desired a changed to his blog's design.
A total of 240 users took the survey on a day when there were 2975 visitors
Sample proportion p= 55%=0.55
q=1-0.55 =0.45
n =240
std error =
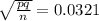
For 90% z value = 1.645
Margin of error =±1.645(0.0032)
=0.0528
=±0.053
A: As the sample size is appropriately large, the margin of error is ±0.053.
D is not right because sample size is not too small, a sample size more than 30 cannot be considered as too small. Also out of 2975 visitors, 240 took survey which seems reasonable size.