Answer: The required slope of the line tangent to the circle at point A is -0.4.
Step-by-step explanation: Given that the radius OA of a circle with center O has a slope of 2.5.
We are to find the slope of the line tangent to the circle at the point A.
We know that
The radius of a circle at a point on the circumference of a circle is perpendicular to the tangent line at the same point on the circumference of the circle.
Also, the product of the slopes of two perpendicular lines is -1.
So, if m is the slope of the tangent line at the point A, then we must have
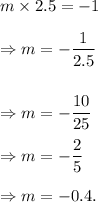
Thus, the required slope of the line tangent to the circle at point A is -0.4.