Question

Radius OA of circle O has a slope of 2.5. What is the slope of the line tangent to circle O to point A?

Answer 1

The tangent at A is perpendicular to OA, so has a slope that is the negative reciprocal of that of the radius: -1/2.5 = -2/5.

Answer 2

Answer: The required slope of the line tangent to the circle at point A is -0.4.

Step-by-step explanation: Given that the radius OA of a circle with center O has a slope of 2.5.

We are to find the slope of the line tangent to the circle at the point A.

We know that

The radius of a circle at a point on the circumference of a circle is perpendicular to the tangent line at the same point on the circumference of the circle.

Also, the product of the slopes of two perpendicular lines is -1.

So, if m is the slope of the tangent line at the point A, then we must have

`m* 2.5=-1\\\\\Rightarrow m=-(1)/(2.5)\\\\\\\Rightarrow m=-(10)/(25)\\\\\Rightarrow m=-(2)/(5)\\\\\Rightarrow m=-0.4.`

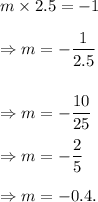
Thus, the required slope of the line tangent to the circle at point A is -0.4.