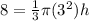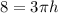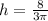Answer:
The height of the cone is
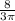
Explanation:
step 1
Find the volume of the cube
The volume of a cube is equal to
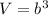
where
b is the length side of the cube
we have
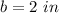
substitute
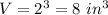
step 2
Find the height of the cone
The volume of the cone is equal to
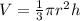
we have
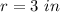
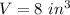 -----> the volume of the cone is equal to the volume of the cube
-----> the volume of the cone is equal to the volume of the cube
substitute the values and solve for h