Question

Boyle’s law states that the volume of a gas varies inversely with applied pressure. Suppose the pressure on 60 cubic meters of gas is raised from 1 atmosphere to 3 atmospheres. what new volume does the gas occupy?

Answer 1

`\bf \qquad \qquad \textit{inverse proportional variation} \\\\ \textit{\underline{y} varies inversely with \underline{x}}\qquad \qquad y=\cfrac{k}{x}\impliedby \begin{array}{llll} k=constant\ of\\ \qquad variation \end{array}\\\\ -------------------------------`


`\bf \stackrel{\textit{the volume of a gas varies inversely with applied pressure}}{v=\cfrac{k}{p}} \\\\\\ \textit{we also know that } \begin{cases} v=60\\ p=1 \end{cases}\implies 60=\cfrac{k}{1}\implies 60=k \\\\\\ \boxed{v=\cfrac{60}{p}} \\\\\\ \stackrel{\textit{now if we apply 3 atmospheres, p=3, what is \underline{v}?}}{v=\cfrac{60}{3}}`

Answer 2

The new volume that the gas occupy is:

20 cubic meters

Explanation:

Boyle’s law states that the volume of a gas varies inversely with applied pressure.

This means that there exist a constant k such that:

`v=(k)/(p)\\\\i.e.\\\\pv=k`

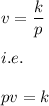
where v is the volume of the gas and is the pressure applied.

This means that if firstly the volume and pressure exerted are:

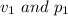`v_1\ and\ p_1` respectively.

and afterwards the pressure applied and the volume of the gas is:

`p_2\ and\ v_2` respectively.

Then by the inverse relation we have:

`p_1v_1=k\\\\and\\\\p_2v_2=k\\\\i.e.\\\\p_1v_1=p_2v_2`

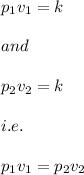
From the data in the question we have:

`v_1=60\ m^3\ ,\ p_1=1\ atm\ ,\p_2=3\ atm`

Hence, we have from equation (1)

`1* 60=3* v_2\\\\i.e.\\\\60=3v_2\\\\i.e.\\\\v_2=(60)/(3)\\\\i.e.\\\\v_2=20\ m^3`