Question

1. The table shows the probabilities of a response chocolate or vanilla when asking a child or adult. Use the formula for conditional probability to determine independence.

a. Are the events “Chocolate” and “Adults” independent? Why or why not?
b. Are the events “Children” and “Chocolate” independent? Why or why not? c. Are the events “Vanilla” and “Children” independent? Why or why not?
Chocolate | Vanilla | Total
Children | 0.14 | 0.26 | 0.40
Adults | 0.21 | 0.39 | 0.60
Total | 0.35 | 0.65 | 1.00

Answer 1

`\begin{matrix}&\text{chocolate}&\text{vanilla}&\text{total}\\\text{children}&0.14&0.26&0.40\\\text{adults}&0.21&0.39&0.60\\\text{total}&0.35&0.65&1.00\end{matrix}`

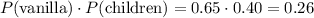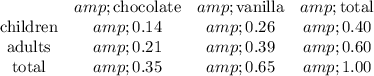
a. "Chocolate" and "Adults" (whatever those mean) will be independent as long as


`P(\text{chocolate}\cap\text{adults})=P(\text{chocolate})\cdot P(\text{adults})`

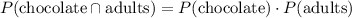
"Chocolate" has the marginal distribution given by the second column, with a total probability of
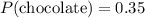
`P(\text{chocolate})=0.35`. Similarly, "Adults" has the marginal distribution described by the third row, so that
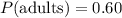
`P(\text{adults})=0.60`. Then


`P(\text{chocolate})\cdot P(\text{adults})=0.35\cdot0.60=0.21`

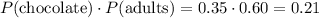
Meanwhile, the joint probability of "Chocolate" and "Adults" is given by the cell in the corresponding row/column, with
`P(\text{chocolate}\cap\text{adults})=0.21`.

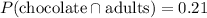
The probabilities match, so these events are indeed independent.

Parts (b) and (c) are checked similarly.

b. Yes;



`P(\text{children})\cdot P(\text{chocolate})=0.40\cdot0.35=0.14`

`P(\text{children}\cap\text{chocolate})=0.14`

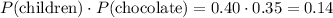
c. Yes;


`P(\text{vanilla})\cdot P(\text{children})=0.65\cdot0.40=0.26`

`P(\text{vanilla}\cap\text{children})=0.26`