Question

The axis of symmetry for the function f(x) = −x2 − 10x + 16 is x = −5. What are the coordinates of the vertex of the graph?

Answer 1

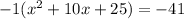
`-1( x^(2) +10x+25)=-41`Do this by completing the square. Start by setting the function equal to 0 and at the same time moving the constant over to the other side of the equals sign.
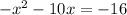
`- x^(2) -10x=-16`. The rules for completing the square is the leading coefficient has to be a positive 1, but ours is -1, so we have to factor out the negative, and when we do that, we have this:
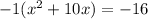
`-1( x^(2) +10x)=-16`. 10x is our linear term. We will take half of tha 10 to get 5, square the 5 to get 25 and add 25 to both sides. HOWEVER, that -1 is still hanging around out front, so what we actually have "added" in is -1(25) = -25. So now what we have is this:
`-1( x^(2) +10x+25)=-16-25.  Simplifying we have [tex]-1( x^(2) +10x+25)=-41`. In this process we have created a perfect square binomial on the left:
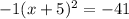
`-1(x+5) ^(2)=-41`. Now we will move the -41 by adding to get
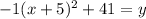
`-1(x+5) ^(2) +41=y`. Our vertex, then, is (-5, 41).

Answer 2

(-5,41)

Explanation:

The axis of symmetry for the function
`f(x) = -x^2 - 10x + 16` is x = -5

Axis of symmetry lies at the x coordinate of vertex

axis of symmetry is x=-5, so the x coordinate of vertex is -5

vertex is (x,y) that is (-5,y)

To find out y we plug in -5 for x in f(x)

`f(-5) = -(-5)^2 - 10(-5)+ 16`

`f(-5) = -25+50+ 16=41`

so the value of y is 41

Vertex is (-5,41)