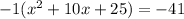
Do this by completing the square. Start by setting the function equal to 0 and at the same time moving the constant over to the other side of the equals sign.
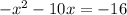
. The rules for completing the square is the leading coefficient has to be a positive 1, but ours is -1, so we have to factor out the negative, and when we do that, we have this:

. 10x is our linear term. We will take half of tha 10 to get 5, square the 5 to get 25 and add 25 to both sides. HOWEVER, that -1 is still hanging around out front, so what we actually have "added" in is -1(25) = -25. So now what we have is this:
![-1( x^(2) +10x+25)=-16-25. Simplifying we have [tex]-1( x^(2) +10x+25)=-41](https://img.qammunity.org/2019/formulas/mathematics/high-school/lptr38tj8a5y0kdmttkrg2601m95e6x5ww.png)
. In this process we have created a perfect square binomial on the left:

. Now we will move the -41 by adding to get
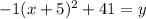
. Our vertex, then, is (-5, 41).