Question

Polygons QRST and Q′R′S′T′ are shown on the following coordinate grid: A coordinate plane with two polygons is shown. Polygon QRST has vertices Q at 3 comma negative 5, R at 2 comma negative 1, S at 5 comma 0, and T at 5 comma negative 4. Polygon Q prime R prime S prime T prime has vertices at Q prime negative 5 comma negative 4, R prime at negative 1 comma negative 3, S prime at 0 comma negative 6, and T prime at negative 4 comma negative 6. What set of transformations is performed on QRST to form Q′R′S′T′? A 180-degree clockwise rotation about the origin followed by a translation 1 unit to the right A 180-degree clockwise rotation about the origin followed by a translation 1 unit to the left A translation 1 unit to the left followed by a 270-degree counterclockwise rotation about the origin A translation 1 unit to the right followed by a 270-degree counterclockwise rotation about the origin

Answer 1

A 270-degree counterclockwise rotation about the origin followed by a translation 2 units to the right.

Explanation:

Answer 2

As you can see from the picture you have:
to rotate point S about the origin by
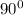
`90^0` clockwise to form point S'';
to rotate point R about the origin by
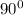
`90^0` clockwise to form point R'';
to rotate point Q about the origin by
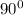
`90^0` clockwise to form point Q'';
to rotate point T about the origin by
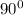
`90^0` clockwise to form point T''.
Then you have to translate polygon Q''R''S''T'' 1 unit down.
Note that rotation
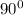
`90^0` clockwise is the same as rotation
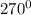
`270^0` counterclockwise, so the correct answer is rotating
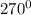
`270^0` counterclockwise about the origin and translating 1 unit down.