As you can see from the picture you have:
to rotate point S about the origin by
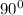
clockwise to form point S'';
to rotate point R about the origin by
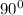
clockwise to form point R'';
to rotate point Q about the origin by
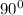
clockwise to form point Q'';
to rotate point T about the origin by
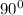
clockwise to form point T''.
Then you have to translate polygon Q''R''S''T'' 1 unit down.
Note that rotation
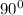
clockwise is the same as rotation
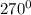
counterclockwise, so the correct answer is rotating
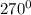
counterclockwise about the origin and translating 1 unit down.