The line passes through points:
(x₁,y₁) = (-1,2)
(x₂,y₂) = (1,-6)
Slope intercept form
y = mx + b
(x,y) stands for one of the points lies on the graph, m stands for the slope of the line, b stands for y-intercept
First, determine the slope of the line (m)m =
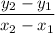
m =
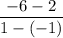
m =
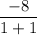
m =
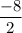
m = -4
Second, determine the value of b (y-intercept)y = mx + b
Use either point (-1,2) or (1,-6) to find b, I use (-1,2)
y = mx + b
2 = -4(-1) + b
2 = 4 + b
2-4 = b
-2 = b
the value of b is -2
Third, form the equation with m = -4 and b = -2y = mx + b
y = -4x - 2 (this is the equation in slope intercept form)