Question

Write in slope-intercept form an equation of the line that passes through the points (−1,2) and (1,−6)

Answer 1

The line passes through points:
(x₁,y₁) = (-1,2)
(x₂,y₂) = (1,-6)

Slope intercept form
y = mx + b
(x,y) stands for one of the points lies on the graph, m stands for the slope of the line, b stands for y-intercept

First, determine the slope of the line (m)
m =
`(y_(2)-y_(1))/(x_(2)-x_(1))`
m =
`(-6-2)/(1-(-1))`
m =
`(-8)/(1+1)`
m =
`(-8)/(2)`
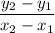
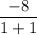
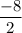
m = -4

Second, determine the value of b (y-intercept)
y = mx + b
Use either point (-1,2) or (1,-6) to find b, I use (-1,2)
y = mx + b
2 = -4(-1) + b
2 = 4 + b
2-4 = b
-2 = b
the value of b is -2

Third, form the equation with m = -4 and b = -2
y = mx + b
y = -4x - 2 (this is the equation in slope intercept form)