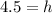So the volume of a sphere is
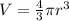
, and the volume of a cone is
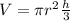
(h=height, r=radius). Knowing only the radius, we can solve for the volume of the sphere. (Also I'm going to be leaving answers in pi form.)
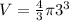
Solve the exponents to get
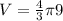
Multiply 4/3 and 9 to get
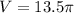
Now that we know the volume of the sphere, we can solve for the height of the cone since the volumes for both are the same.

Solve the exponents to get
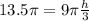
Divide
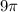
on each side to get

Multiply 3 on each side, and your answer should be