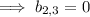Answer: 0
Explanation:
Two matrix are called equal to each other if they have the same dimension and every element of one element is same as the every element of the another.
Here, Matrix A and Matrix B are equal to each other,
Where,
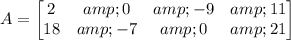
Which having 2 rows and 4 columns, or having dimension 2 × 4
Thus, the dimension of matrix B = 2 × 4
Also, the third element of the second row of matrix A,
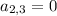
If b represents the element of matrix B,
Thus by the above definition,