1. Remember that the perimeter is the sum of the lengths of the sides of a figure.To solve this, we are going to use the distance formula:
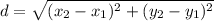
where
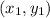
are the coordinates of the first point
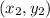
are the coordinates of the second point
Length of WZ:
We know form our graph that the coordinates of our first point, W, are (1,0) and the coordinates of the second point, Z, are (4,2). Using the distance formula:
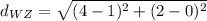
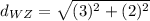
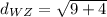
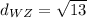
We know that all the sides of a rhombus have the same length, so
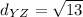
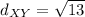
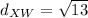
Now, we just need to add the four sides to get the perimeter of our rhombus:
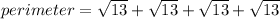
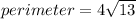 We can conclude that the perimeter of our rhombus is
We can conclude that the perimeter of our rhombus is 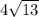 square units.
square units.
2. To solve this, we are going to use the arc length formula:
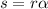
where

is the length of the arc.

is the radius of the circle.
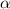
is the central angle in radians
We know form our problem that the length of arc PQ is
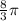
inches, so
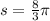
, and we can infer from our picture that
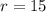
. Lest replace the values in our formula to find the central angle POQ:
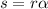
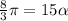
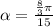
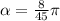 Since
Since 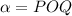
,
We can conclude that the measure of the central angle POQ is 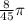 3.
3. A cross section is the shape you get when you make a cut thought a 3 dimensional figure. A rectangular cross section is a cross section in the shape of a rectangle. To get a rectangular cross section of a particular 3 dimensional figure, you need to cut in an specific way. For example, a rectangular pyramid cut by a plane parallel to its base, will always give us a rectangular cross section.
We can conclude that the draw of our cross section is: