The first thing we must do for this case is to define variables.
We have then:
x: price of adult's ticket
y: price of child's ticket
We now write the system of equations:
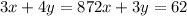
Solving the system of equations we have:
x = 13 $
y = 12 $
Answer:
the price of adults ticket and price of child's ticket are $ 13 and $ 12, respectively