Question

Write an equation parallel to the line

Answer 1

In case of parallel lines

`(a1)/(a2) = (b1)/(b2) \: not \: equal \: to \: (c1)/(c2)`
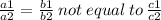
Where a1, b1 and c1 are the constants of the first equation and a2, b2 and c2 are the constants of the second equation
From first equation (5x+10y+4 = 0)
a1 = 5
b1 = 10
c1 = 4
So now what we want to do is to divide 5 by a number and 10 by another number to get the same result at the end
I'll divide 5 by 1 and 10 by 2 to get the same number 5
5/1 = 10/2
Then I'll divide 4 by any number to get a result other than 5
Let's say 4 (or any other number it can be positive as well as negative)
So
a2 = 1
b2 = 2
c2 = 4
Then now the last step is to write the equation using these constants
x + 2y +4 =0
x+2y= - 4
Therefore this equation is parallel to 5x+10y = - 4

Answer 2

The easiest way to find a parallel equation is to write your equation in slope-intercept form. The general equation for slope-intercept form is y = mx + b, where m = the slope of the equation, b = the y intercept, and x and y are your variables.

You're given 5x + 10y = -4.
1) Move 5x to the right side by subtracting 5x from both sides:
5x + 10y = -4
10y = -5x - 4

2) Divide both sides by 10 to get y by itself on the left. Simplify:

`10y = -5x - 4\\ y = - (5)/(10) x - (4)/(10) \\ y = - (1)/(2) x - (2)/(5)`



Remember that for parallel lines, the slope, m, is the same for both equations. You can make the y-intercept, b, whatever number you want.

When the equation is in slope-intercept form,
`y = - (1)/(2) x - (2)/(5)`, you can see that
`m = - (1)/(2)`.

A parallel equation is in the form:

`y = - (1)/(2) x + b`

Plug in anything you want for b. One example is:
`y = - (1)/(2) x + 3`

-------

Answer:
`y = - (1)/(2) x + 3` (just one example)