You can break down the image into the triangle and semicircle, find the area of each, and add the areas together to get the total area of the figure.
1) Area of triangleThe equation for the area of a triangle is:
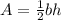
where A = area, b = length of base, and h = height of triangle.
Looking at the attached picture, the base (green line), b = 8, and the height (blue dashed line), h = 4. Plug these values into
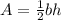
.
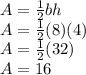 2) Area of semicircle
2) Area of semicircle
The equation of the area of a semicircle is simply the area of the circle divided by 2, making the equation:
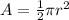
where A = area and r = radius of the circle.
The radius of the circle is half of the diameter (green line in picture). That means the radius, r = 8/2 = 4. Plug that into the equation and solve for area of the semicircle:
 3) Add the areas of the triangle and semicircle together
3) Add the areas of the triangle and semicircle together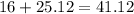
-------
Answer: 41.12