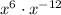Question

Which could be the first step in simplifying this expression? Check all that apply. (x^3 x^-6)^2

(x^-18)^2
(x^-3)^2
(x^-2)^2
x^6 x^-12
x^5 x^-4

Answer 1

x^(3 + (-6) )= (x^-3)^2

Answer 2

Option B and D are correct

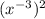`(x^(-3))^2` or

`x^6 \cdot x^(-12)`

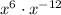
Explanation:

Using exponent rule:

`(ab)^m = a^m \cdot b^m`

`(a^m)^n = a^(mn)`

`a^m \cdot a^n = a^(m+n)`

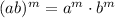
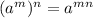
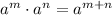
Given the expression:

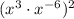`(x^3 \cdot x^(-6))^2` ....[1]

Apply the exponent rule:

`(x^(3-6))^2`

`(x^(-3))^2`

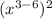
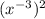
We can write the given expression as:

Apply the exponent rule in [1]:

`(x^3)^2 \cdot (x^(-6))^2`

⇒
`x^6 \cdot x^(-12)`

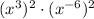
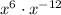
Therefore, the first step in simplifying this expression are:

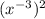`(x^(-3))^2` or
`x^6 \cdot x^(-12)`