Question

John has taken out a loan for college. He started paying off the loan with a first payment of $100. Each month he pays, he wants to pay back 1.1 times as the amount he paid the month betore. Explain to Jo howto represent his first 20 payment n sigma notation.Then esplain how to tind the sum of his frst 20 pyments, using complete sentences. Esplain why this series is convergent or divergent

Answer 1

Since each term of the series is 1.1 times the previous one, the series is geometric. The generic term of a geometric series is

`a_(n)=a_(0)\cdot r^((n-1))`

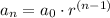
The sum in sigma notation simply adds these terms. The leading factor of 100 can be factored out.

`sum=\displayform{100\cdot\sum\limits_(n=1)^(20){1.1^((n-1))}}`

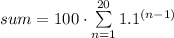
The sum can be found by adding the terms or by using the formula for the sum of a geometric series. In the latter case, we have

`sum=100\cdot(1.1^(20)-1)/(1.1-1)\approx5727.50`

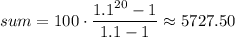
The series is divergent because the common ratio of terms is greater than 1. (Of course, any finite number of terms will have a finite sum.)