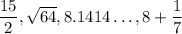First, some rewriting:

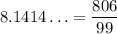
Why? If
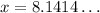
, then
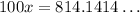
, which means
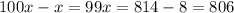
, and so
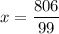
.
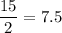
So from the four given numbers, it's obvious that
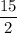
is the smallest, followed by
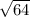
. So you just need to determine which of
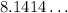
and
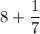
is smallest.
Note that
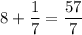
To easily compare this number to
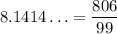
, we need to find a common denominator. The greatest common divisor of 7 and 99 is 1 (they are relatively prime), so
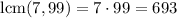
. So we write
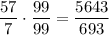
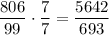
So we find that
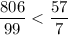
, that is,
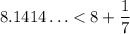
.
So the proper ordering from least to greatest is