Answer:
Option b -
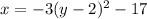
Explanation:
Given : A parabola that opens to the left with vertex (-17,2).
To find : Which of the following could be the equation for a parabola?
Solution :
The general form of the parabola that opens to the left i.e. horizontal is given by :
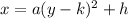
Where, (h,k) are the vertex of the parabola
and a is negative because parabola opens left.
We have given the vertex (-17,2)=(h,k)
The rough equation of the parabola is
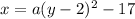
The only option matches with our equation is option b.
Therefore, The required form of the parabola is
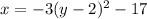
So, Option b is correct.