Question

Which of the following could be the equation for a parabola that opens to the left with vertex (-17,2)?

a. y=3(x+17)^2+2
b. x=-3(y-2)^2-17
c. x=3(y+17)^2+2
d. y=3(x-2)^2-17

Answer 1

A sideways opening parabola is in the form
`x= y^(2)`, so we know from the process of elimination that it will either be b or c. Next we have to realize that if the parabola opens to the left it is a negative parabola, just like if a parabola opens upside down it is a negative parabola. So the one that has the negative out front is b.

Answer 2

Option b -
`x=-3(y-2)^2-17`

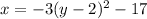
Explanation:

Given : A parabola that opens to the left with vertex (-17,2).

To find : Which of the following could be the equation for a parabola?

Solution :

The general form of the parabola that opens to the left i.e. horizontal is given by :

`x=a(y-k)^2+h`

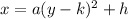
Where, (h,k) are the vertex of the parabola

and a is negative because parabola opens left.

We have given the vertex (-17,2)=(h,k)

The rough equation of the parabola is
`x=a(y-2)^2-17`

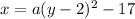
The only option matches with our equation is option b.

Therefore, The required form of the parabola is
`x=-3(y-2)^2-17`

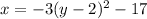
So, Option b is correct.