Question

The formula S = A((1+r)t+1−1r) S = A 1 + r t + 1 - 1 r models the value of a retirement account, where A = the number of dollars added to the retirement account each year, r = the annual interest rate, and S = the value of the retirement account after t years. If the interest rate is 11%, how much will the account be worth after 15 years if $2200 is added each year? Round to the nearest whole number.

Answer 1

$86217.8866411

Explanation:

Formula :
`S=A((1+r)^((1+t))-1)/(r)`

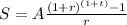
Where

A = the number of dollars added to the retirement account each year

r = the annual interest rate

S = the value of the retirement account after t years.

Given :

interest rate r= 11% =0.11

Amount (A) = $2200

Time(t) = 15 years

Substituting values in the formula :

`S=2200((1+0.11)^((1+15))-1)/(0.11)`

`S=86217.8866411`

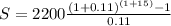
Thus the account will be worth $86217.8866411 after 15 years if $2200 is added each year.

Answer 2

So this is how you will arrive to the answer:

The following formula models the value of a retirement account,

S = (A [ ( 1 + r ) ^ (t + 1) - 1] / r)

wherein:

A = number of dollars added to the retirement account (each year)

r = annual interest rate

s = value of the retirement account after t years

The question is:

If the interest rate is 11% then how much will the account be worth after 15 years if $2200 is added each year?

Round to the nearest whole number.

Solution:

The said formula contains the term t + 1 instead of the usual "t". Means that the formula applies only in the situation where the money is invested at the beginning of the year instead of the usual practice at the end

Given:

A = 2200
r = 0.11
t = 15

The accumulated amount:
F = A ((1 + r) ^ (t+1) - 1 / r

Substitute:

F = 2200 (1.11 ^ (15 + 1 ) - 1) /0.11
F = 86217.88664

If money is invested at the end of the year, then F = 80476.49, the difference being the investment of an extra 2200 over 15 years.