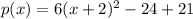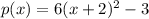Question

Write p(x) = 21 + 24x + 6x2 in vertex form. p(x) =___ (x +__ )2 – ___

Answer 1

vertex form is
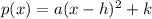
`p(x)=a(x-h)^2+k`basically, just complete the square on the right side

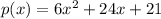
`p(x)=6x^2+24x+21`group x terms together

`p(x)=(6x^2+24x)+21`
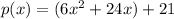
factor out linear coefient (number in front of the higest power x, in this case x^2)

`p(x)=6(x^2+4x)+21`
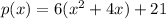
take 1/2 of the linear coefient and square it (4 is linear coefient so take 1/2 of it and square it (4/2=4, 4^2=4)), add positive and negative of it inside the parenthaees (so it equals 0)

`p(x)=6(x^2+4x+4-4)+21`
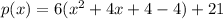
factor perfect square trinomial
`p(x)=6((x+2)^2-4)+21`
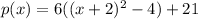
distribute (don't distribute or expand the squared term)
`p(x)=6(x+2)^2-24+21`

`p(x)=6(x+2)^2-3`

Answer 2

6,2,3

Explanation: