We want an integer

such that
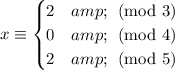
Note that the moduli are all relatively prime, so we can use the Chinese remainder theorem right away. As a first step, let's suppose
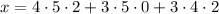
Taken modulo 3, the last two terms immediately vanish, and
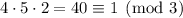
. We want a remainder of 2, so we just multiply this term by 2.
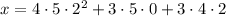
Next, taken modulo 4, all terms vanish, so we're good here.
Then, taken modulo 5, the first two terms vanish and we're left with
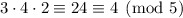
. We want a remainder of 2. To rectify this, we can first multiply this term by the inverse of 4 modulo 5, then multiply again by 2. This guarantees that
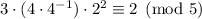
The inverse of 4 modulo 5 is 4, since
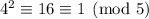
, so we end up with
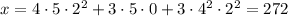
You can confirm for yourself that 272 satisfies the desired conditions. The CRT says that any integer of the form
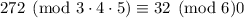
will work, i.e.
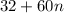
where

, and in particular 32 is the smallest positive solution.