Question

Find an integer that leaves a remainder of 2 when divided by either 3 or 5, but that is divisible by 4.

Answer 1

We want an integer
`x` such that


`x\equiv\begin{cases}2&\pmod3\\0&\pmod4\\2&\pmod5\end{cases}`

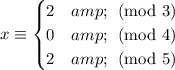
Note that the moduli are all relatively prime, so we can use the Chinese remainder theorem right away. As a first step, let's suppose


`x=4\cdot5\cdot2+3\cdot5\cdot0+3\cdot4\cdot2`

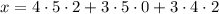
Taken modulo 3, the last two terms immediately vanish, and
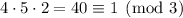
`4\cdot5\cdot2=40\equiv1\pmod3`. We want a remainder of 2, so we just multiply this term by 2.


`x=4\cdot5\cdot2^2+3\cdot5\cdot0+3\cdot4\cdot2`

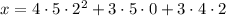
Next, taken modulo 4, all terms vanish, so we're good here.
Then, taken modulo 5, the first two terms vanish and we're left with
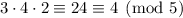
`3\cdot4\cdot2\equiv24\equiv4\pmod5`. We want a remainder of 2. To rectify this, we can first multiply this term by the inverse of 4 modulo 5, then multiply again by 2. This guarantees that



`3\cdot(4\cdot4^(-1))\cdot2^2\equiv2\pmod5`

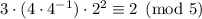
The inverse of 4 modulo 5 is 4, since
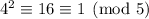
`4^2\equiv16\equiv1\pmod5`, so we end up with


`x=4\cdot5\cdot2^2+3\cdot5\cdot0+3\cdot4^2\cdot2^2=272`

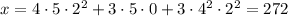
You can confirm for yourself that 272 satisfies the desired conditions. The CRT says that any integer of the form



`272\pmod{3\cdot4\cdot5}\equiv32\pmod60`

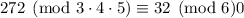
will work, i.e.
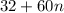
`32+60n` where
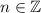
`n\in\mathbb Z`, and in particular 32 is the smallest positive solution.