Question

PLEASE I NEED HELP

what is the equation of the circle with center (-4 -3) that passes through the point (6,2)

Answer 1

The equation for a circle in standard form is
`(x-h) ^(2)+(y-k) ^(2) = r^(2)`. We have the center, so we have the h and the k, and we have a point, so we have the x and the y. Let's fill in accordingly and simplify.
`(6-(-4)) ^(2) +(2-(-3)) ^(2) = r^(2)`. Solving for
`r^(2)`, we get that
`r^(2) =125`, Now we can use the info given plus our newly found radius and write the equation.
`(x+4) ^(2) +(y+3) ^(2) =125`

Answer 2

The general equation of the circle is:


`(x-h)^(2) +(y-k)^(2) =r^(2)`

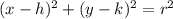
(h,k) is the center of the circle and r is the radius. We are given the coordinates of the center. So we can write the equation of the circle as:


`(x+4)^(2) +(y+3)^(2) =r^(2)`

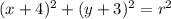
In order to complete the equation, we need the radius of the circle. Using the given point we can find the radius. Using the point in the above equation, we get:


`(6+4)^(2)+(2+3)^(2)=r^(2) \\ \\ 100+25=r^(2)`

Thus the value of r² is 125. Using the value in equation of the circle, we get:


`(x+4)^(2) +(y+3)^(2) =125`

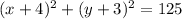
The radius of the circle is √125.