The general equation of the circle is:
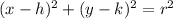
(h,k) is the center of the circle and r is the radius. We are given the coordinates of the center. So we can write the equation of the circle as:
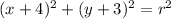
In order to complete the equation, we need the radius of the circle. Using the given point we can find the radius. Using the point in the above equation, we get:
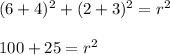
Thus the value of r² is 125. Using the value in equation of the circle, we get:
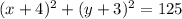
The radius of the circle is √125.