Answer:
2 triangles are possible.
Explanation:
Given,
In triangle ABC,
∠ B = 45°,
AC = b = 4 unit,
AB = c = 5 unit,
By the sine law,
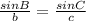
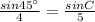
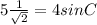
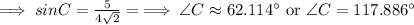
If ∠C = 62.114°,
∵ ∠A + ∠B + ∠C = 180°,
∠A + 45° + 62.114° = 180°
⇒ ∠A = 72.886°,
If ∠C = 117.886°
⇒ ∠A + 45° + 117.886° = 180°
⇒ ∠A = 17.114°,
Again by the law of sine,
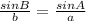
If ∠A = 72.886°,
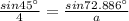
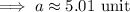
If ∠A = 17.114°,
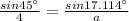
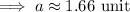
Hence, two triangles are possible.