Question

Determine the number of possible triangles, ABC, that can be formed given B = 45°, b = 4, and c = 5. 0 1 2

Answer 1

There are 2 triangles that exist within this single triangle. It is an SSA triangle, so it is the case of the ambiguous triangle. Sounds scary. You have to drop an altitude and find out what the height of it is. You can use the sin45 = h/5 to find that the height is 3.5. The rule for this is if the height is smaller than b and b is smaller than c, you have 2 triangles. That is true here, so you have 2 triangles. Solving both of them involves the Law of Sines and the rules of supplementary angles...a whole 'nother type of pain in the butt.

Answer 2

2 triangles are possible.

Explanation:

Given,

In triangle ABC,

∠ B = 45°,

AC = b = 4 unit,

AB = c = 5 unit,

By the sine law,

`(sin B)/(b)=(sin C)/(c)`

`(sin 45^(\circ))/(4)=(sin C)/(5)`

`5 (1)/(√(2)) = 4 sin C`

`\implies sin C = (5)/(4√(2)) =\implies \angle C\approx 62.114^(\circ)\text{ or }\angle C=117.886^(\circ)`

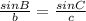
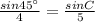
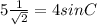
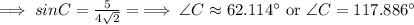
If ∠C = 62.114°,

∵ ∠A + ∠B + ∠C = 180°,

∠A + 45° + 62.114° = 180°

⇒ ∠A = 72.886°,

If ∠C = 117.886°

⇒ ∠A + 45° + 117.886° = 180°

⇒ ∠A = 17.114°,

Again by the law of sine,

`(sin B)/(b)=(sin A)/(a)`

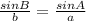
If ∠A = 72.886°,

`(sin 45^(\circ))/(4)=(sin 72.886^(\circ))/(a)`

`\implies a\approx 5.01\text{ unit}`

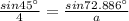
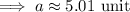
If ∠A = 17.114°,

`(sin 45^(\circ))/(4)=(sin 17.114^(\circ))/(a)`

`\implies a\approx 1.66\text{ unit}`

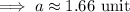
Hence, two triangles are possible.