For a better understanding of the solution please find the diagram in the attached file.
The diagram is that of a triangular part of the regular polygon. The triangle
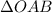 is an isosceles triangle because the sides OA and OB are equal. Now, The angle
is an isosceles triangle because the sides OA and OB are equal. Now, The angle
 . This is because the angle around the central angle of a polygon is 360 degrees in total.
. This is because the angle around the central angle of a polygon is 360 degrees in total.
Now, because
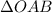 is an isosceles triangle, angle OAP will be half of angle OAB. Thus,
is an isosceles triangle, angle OAP will be half of angle OAB. Thus,
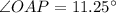 .
.
AP will be half of AB. Therefore, AP=2.
Now, the apothem, OP can thus be found as:
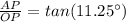
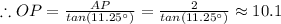
Thus the area of one triangle is

Therefore, the area of all the 16 triangles that make up the regular polygon is:
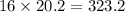
Thus the area of the polygon is 323.2 squared inches.