You have to use the Law of Cosines twice here. Let's find angle A first:
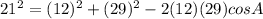
. Doing a bit of simplifying you get
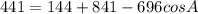
. Simplifying a bit more gives you -544=-696cosA. cosA = .78160919 and that A = 38.6. Actually, now that I think about it we can now move to the Law of Sines to find another angle because the triangle is not a right triangle. Just trust me. Let's find angle B now.
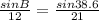
and that
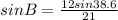
. sinB = .3565026267 and that angle B is 20.9. Knowing those 2 angles we can find C: 180-38.6-20.9=120.5 and there you have it.