Answer: The correct option is (C)
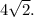
Step-by-step explanation: We are given to find the length of side 's' of the square shown in the figure.
We know that
all the four sides of a square are equal in length and all the four angles are right angles.
So, each of the two equal parts of the square form a right-angled triangle with hypotenuse as the diagonal.
Therefore, using Pythagoras theorem in one of the right-triangles, we get
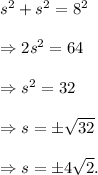
Since the length of a side of a square cannot be negative, so we get
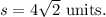
Option (C) is CORRECT.